Data Structure 19 B Tree & B+ Tree

Before：Long Time No See Guys!~ I’ve been busy struggling with my Maths Analysis,Physics and Mathematical Logic learning,also busy building connections with others.But I realize that I have to keep learning my data structure in order to start B Plus Tree as soon as possible.

记得她泪水涟涟

Data Structure 19 外部查找与排序

主存储器与外存储器

主存储器与外存储器是计算机的两类不同存储物质。主存储器也称内存，用于存储正在运行的的程序代码及运行数据。外存储器用于存储长期保存的信息，常用的外存储器有磁盘、磁带、光盘、U盘。

相比于内存，外存储器有价格低廉、存储址大和永久保存等优点。但也有访问速度慢的缺点。在考虑处理外存储器上数据的算法时应该重点考虑如何减少访问次数。

磁盘是一种可以直接存取的外存设备，它不仅可以顺序存取，也可以直接存取。它的存取速度比磁带快得多。磁盘表面上有很多同心圆的轨道，称为磁道，信息被存储在磁道上。所有磁盘上的同一位置的磁道称为一个柱面。每条磁道又被分成若干段，每一段称为一个扇区。一个扇区相当于磁带上的一个数据块，也称为磁盘块，是一次磁盘读写的单位。

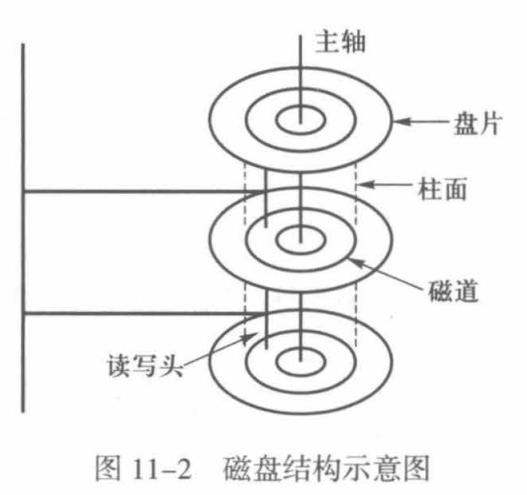
一次磁盘访问所需的时间相当于执行几百万条甚至几千万条指令所需的时间😰。由于磁盘和磁带的访问特性，在设计基于外存的箕法时，宁愿做很多的计算来避免一次外存访问。在包含外存操作的情况下，外存访问的次数决定了操作的运行时间。外存访问次数要能减半，运行时间也就减半了。

B树

B树的定义

提高外存储器中查找表的查找效率，最直接的方法就是减少磁盘访问的次数。在查找树中，访问的次数与查找树的高度成正比。在外存储器中，每次访问对应了一次磁盘访问。
因此，要减少磁盘访问次数，必须降低查找树的高度。解决方案也很简单：只需要增加树的分支。一棵M叉查找树的高度约为$log_M N$

在M叉查找树中，我们同样需要保存M - 1个键来判断到哪个分支继续操作。同时，为了保证最坏情况下依然具有高效性，我们需要一些措施来保证M叉查找树的平衡。

1970 年，R.Bayer 和 E.Macreight 提出了 B 树的概念。B 树是一棵平衡的 m 叉的查找树，主要被用作为大型文件的索引。B 树的定义如下：
一棵M阶B树或者为空，或者满足以下条件：

• 根结点要么是叶子，要么至少有2个儿子，至多有M个儿子
• 除根结点和叶结点之外，每个结点的的儿子个数s满足[ m/2 ]$\leq s\leq$m
• 有s个儿子的非叶结点具有n = s - 1个关键字，故s = n + 1.
  这些结点的数据信息为：(n,$A_0$,($K_1$,$R_1$),$A_1$,($K_2$,$R_2$),$A_2$,…,($K_n$,$R_n$),$A_n$)
  其中：
  n：关键字个数
  $K_i$：结点的关键字
  $A_0$：B树中小于$K_1$的结点地址
  $R_j$：关键字值等于$K_j$的数据记录在硬盘中的地址
  $A_j$：B树中大于$K_j$小于$K_{j + 1}$的结点的地址
  $A_n$：B树中大于$K_n$的结点的地址
• 所有的叶子结点都出现在同一层上（深度相同），并且不带信息（可以认为是查找失败的结点）

一次磁盘读写可以读入磁盘上的一个块。因此，在B树的设计中可以将一个磁盘块作为一个B树的结点，根据磁盘块的大小、关键字的长度以及磁盘块地址的长度决定 B 树的阶数。

B树的查找

和BST的查找操作类似，只是抛弃了更多的branch

B树的插入

插入操作以查找操作为基础。
首先在m阶B树上进行查找操作，确定新插入的关键字key在最底层的非叶结点的插入位置。若被插入结点的关键字个数小于m-1，则插入操作结束；若该结点原有的关键字个数已经等于m-1，必须分裂成2个结点。

设在插入关键字key之前，结点（设其原地址为p）原来为：
(m - 1,$A_0$,($K_1$,$R_1$),$A_1$,($K_2$,$R_2$),$A_2$,…,($K_{m - 1}$,$R_{m - 1}$),$A_{m - 1}$)

则在插入一个新关键字key后变为：
(m,$A_0$,($K_1$,$R_1$),$A_1$,($K_2$,$R_2$),$A_2$,…,($K_m$,$R_m$),$A_m$)

由于结点的关键字数量个数已经超过了最大值m-1，所以必须进行分裂。这样，就必须创建一个新的结点，设该结点地址为q，它将包括第ceil(m/2) + 1个关键字到第m个关键字和相应的指针信息，这些信息可以从地址为p的结点中复制过来。这样的结点形式为：
(m - ceil(m/2),$A_{ceil(m/2)}$,($K_{ceil(m/2) + 1}$,$R_{ceil(m/2) + 1}$),…,($K_{m}$,$R_{m}$),$A_{m}$)

同样原结点也需要进行更新，第ceil(m/2) + 1个关键字到第m个关键字和相应的指针信息需要被删除，得到的新的结点p为：
(ceil(m/2) - 1,$A_0$,($K_1$,$R_1$),$A_1$,($K_2$,$R_2$),$A_2$,…,($K_{ceil(m/2) - 1}$,$R_{ceil(m/2) - 1}$),$A_{ceil(m/2) - 1}$)

关键字($K_{ceil(m/2)}$,$R_{ceil(m/2)}$)插入父结点的位置中。

新关键字的插入将导致父结点的关键字个数增加一个。如果父结点的关键字个数本来就为最大值 m-1 ，那么又会导致新一轮的结点分裂，这样有可能分裂一直进行到根结点为止。在根结点这一层上，可能创建一个新的根结点，导致 B 树长高一层。

B树的删除

删除操作同样类似于BST的删除操作，同样采用了“替身”的方法以保证树的完整性。

删除时，从根结点开始查找与给定关键字值 key 相等的关键字$K_i$。关键字 $K_i$ 可能出现在第一层到最底层之间的任何一个结点上，我们分以下几种情况讨论：
（1）如果关键字$K_i$在最底层，可直接删除，转（3）
（2）否则，先找替身。用它的右子树的最左面的结点的关键字值（即处于最底部层上的最小关键字值代替），然后删除最底层上的该关键字。
（3）从最底层开始进行删除相关关键字的操作，有以下几种情况：

• 若删除关键字之后，结点的关键字的个数仍处于 ceil(m/2)-1 和 m-1 之间，仍满足 B 树的结点的定义，删除结束。
• 若结点的关键字的个数原为ceil(m/2) - 1 ，若再删除一个关键字，将不符合 B 树定义。如果该结点的左或右兄弟结点的关键字的个数大于ceil(m/2) - 1 ，则借一个关键字过来。如果是借左兄弟结点的最大关键字，则必须将该关键字上移到父结点的相应位置，而将父结点中大于该关键字且最接近该关键字的那个关键字（连同左兄弟结点的最右方的指针 An）下移到被删关键字所在结点的最左面，删除操作结束。若借右兄弟结点的最小关键字，操作类似。
• 该结点的左或右兄弟结点的关键字的个数都为ceil(m/2)-1，那么将无结点可借。这时只能执行合并结点的操作。将该结点同左兄弟（无左兄弟时，与右兄弟）合并。由于两个结点合并后，父结点中相应的关键字将不再保留，因为它原来的左右儿子已经不存在，因此，把父结点中该关键字也并入合并后的结点。这样，父结点的关键字个数便减少了一个。如果父结点的关键字个数不满足定义，则必须继续调整，最坏情况下可能达到根结点，使B树减少一层。

B+树

B+树的定义

B树能快速支持查找某个记录，但如果要对整个文件中的记录按关键字的递增顺序进行访问，则时间是灾难性的。既能支持每个记录的随机访问也能支持对整个文件按关键字次序访问的文件称为索引顺序文件。这个索引结构称为B+树，这是目前文件系统和数据库系统中应用广泛的索引结构。

文件可以看成一个驻留在外存储器上的数组 。要保待数组中元素的有序性，在插入或删除时将引起大量的数据记录的移动。而文件中的数据量是非常大的，这个移动将是灾难性的。

B+树采用了允许每一块不放满数据的策略，使得插入和删除时只影响记录所在的数据块，而不会影响其他数据块。

鉴于B+树既要考虑到索引的组织，又要考虑到记录本身的存放，M 阶的B+树被定义为具有以下性质的 M 叉树：

• 根要么是叶子，要么有2到M个孩子
• 除根之外的结点都有不少于ceil(M/2)且不多于M个孩子
• 有k个孩子的结点保存了k-1个键来引导查找，键i代表子树i+1中键的最小值
• 叶结点中的孩子指针指向存储记录的数据块的地址。换句话说，对于索引B+树，它们是叶结点。但对于数据块来说，它们又是数据块的父结点。数据块才是真正的叶结点。而在B树中，叶结点的孩子指针都是空指针。
• 每个数据块至少有ceil(L/2)个记录，至多有L个记录。

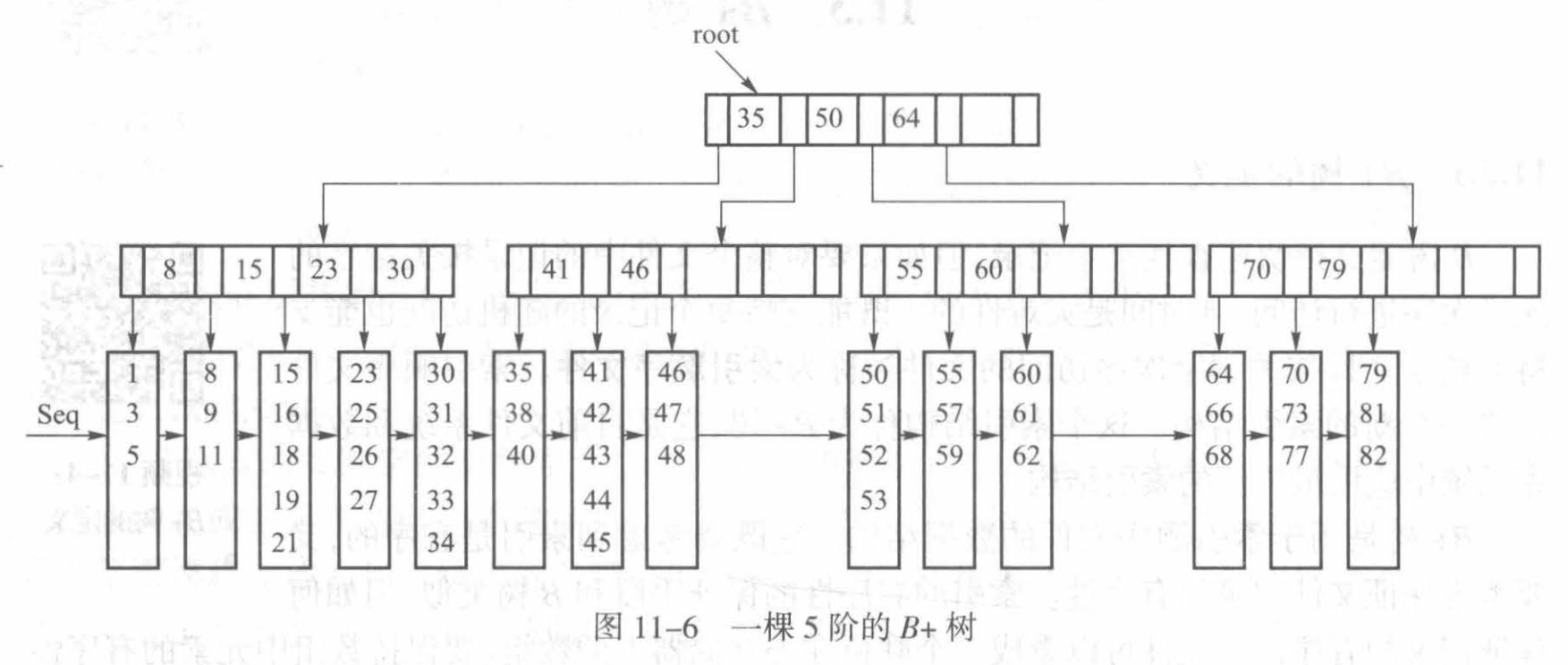
为了提高磁盘访问的效率，每个结点的大小也是一个磁盘块，这样一次磁盘读写正好读写一个完整的结点。

B+树的查找

类似BPT、B Tree等，不赘述了

B+树的插入

B+树的插入过程也与二叉查找树类似。先从根结点开始查找插入的位置，把它插入相应的数据块中。但问题是存储记录的数据块中记录数是有限的，当插入遇到数据块已满时，必须有特殊的处理。

特殊处理与B树的处理类似（相当类似）

B+树的删除

删除时，首先要找到存储被删记录的结点，然后再在结点中删除它。但问题在于如果此时结点中的记录数量只满足要求的最小值，再删除一个记录就不再满足要求了。此时如果邻居结点的记录数不是最少，就借一个过来领养，如果邻居结点的记录数也是最少，就把两个结点合并成一个满的结点。很不幸的是这种情况出现时，父亲就失去了一个孩子，而如果此时父亲的孩子数也少于最小值了，就使用同样的策略了，一直向根进行过滤。而这时根可能只有一个孩子了。如果真的是这样，就把根给删除了，让它的孩子作为新的根。这也是唯一能使 B＋树变矮的情况。