数据结构 10 Basic Graphics

Before：Start Of Graphics!虽然并非想象中组合数学里的图论，但，但，但至少是图吧。当年学竞赛的时候总觉得组合题很fasinating，但也真的是不会做，甚至有时候答案都猜不出来…

总觉得自己想额外做好多事，所以把各种ddl早早地清掉，但好像还是每天都很忙，还是没什么时间玩儿自己真正想玩儿的东西😇

数据结构 10 图的基本概念

图的定义

多对多的关系

图可以用G=(V, E)表示

• V是顶点的集合，顶点代表数据元素，即V是数据元素集合
• E是连接顶点的边的集合，边代表元素间的关系，即E是关系的集合

分为：

• 有向图
• 无向图
• 加权图：边被赋予一个权值，表示关系的程度
• 完全图：任意两个结点之间都有边的无向图称为完全图；每两个结点之间都有两条弧的有向图称为有向完全图。

基本术语：

• 度：图中连接于某一结点的边的总数
• 入度：有向图中进入某一结点的边数，称为该结点的入度
• 出度：有向图中离开某一结点的边数，称为该结点的出度
• 子图：设有两个图G=（V，E）和G‘=（V’，E’），如果 V’$\subset$ V，E’$\subset$ E 则称G’是G的子图
• 路径：用一个结点序列w1,w2,……wN
• 简单路径：如果一条路径上的所有结点，除了起始结点和终止结点可能相同外，其余的结点都不相同，则称其为简单路径。
• 环：环是一条简单路径，其起始结点和终止结点相同，且路径长度至少为1。
• 非加权的路径长度：组成路径的边数，对于路径w1,w2,……wN ，非加权路径长度为N-1
• 加权路径长度：路径上所有边的权值之和
• 连通：顶点v至v’ 之间有路径存在
• 连通图：无向图 G 的任意两点之间都是连通的，则称 G 是连通图。
• 连通分量：非连通图中的极大连通子图
• 强连通图：有向图 G 的任意两点之间都是连通的，则称 G 是强连通图。
• 强连通分量：极大连通子图
• 弱连通图：如有向图G不是强连通的，但如果把它看成是无向图时是连通的，则称该图是弱连通的。
• 生成树：连通图的极小连通子图。包含图的所有 n 个结点，但只含图的 n-1 条边。在生成树中添加一条边之后，必定会形成回路或环。

在图论中，树其实是连通、无环路的图

其他结构都可以看成是图的特例，一个特殊的有向图

• 集合结构：边集为空
• 线性结构：有向无环图。除起始结点和终止结点外，每个结点的入度出度均为1。起始结点入度为0，终止结点出度为0
• 树状结构：有向无环图。除根结点外，每个结点入度为1，出度为0 ~ N。根结点入度为0

图的存储

邻接矩阵

• 顶点集合：存储在一个数组中
• 边集合：用 n 行 n 列的布尔矩阵 A 表示。如果i 至 j 有一条有向边，A[i,j] = 1 ，如果 i 至 j 没有一条有向边，A[i,j] = 0。

从定义可以看出，邻接矩阵的优缺点都很明显：

• 优点：O(1)乱杀
• 缺点：对于稀疏图（也是大多数图），太占内存空间
  于是我们想到——链表！！！

邻接表

• 顶点集合：用数组或单链表的形式存放所有的结点值
  如果结点数n固定，则采用数组形式，否则可采用单链表的形式
• 边集合：同一个结点出发的所有边组成一个单链表

存储示意图：

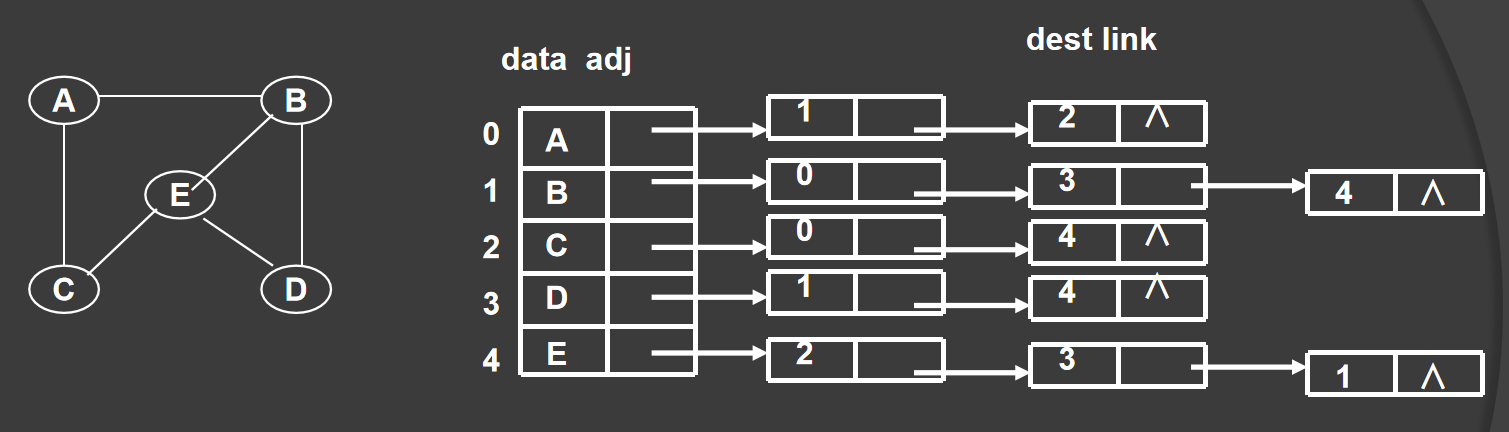
邻接表定义

横向的单链表和纵向的单链表

template <class TypeOfVer, class TypeOfEdge>
class adjListGraph:public graph<TypeOfVer,TypeOfEdge>{
public:      
    adjListGraph(int vSize, const TypeOfVer d[]);
    void insert(TypeOfVer x, TypeOfVer y, TypeOfEdge w);
    void remove(TypeOfVer x, TypeOfVer y);
    bool exist(TypeOfVer x, TypeOfVer y) const;
    ~adjListGraph();

private:
    struct edgeNode{  //存储边的结点类型
        int end; //终点
        TypeOfEdge weight; //权值
        edgeNode *next;
        edgeNode(int e,TypeOfEdge w,edgeNode *n = nullptr):end(e),weight(w),next(n){}
    };

    struct verNode{  //保存结点的数据类型
        TypeOfVer ver; //顶点值
        edgeNode *head;  //edgeNode数组
        verNode(edgeNode *h = nullptr):head(h){}
    };

    verNode *verlist;

    int find(TypeOfVer v) const{
        for(int i = 0;i < Vers;i ++){
            if(verlist[i] == v){
                return i;
            }
        }
    }
}

构造函数

template <class TypeOfVer, class TypeOfEdge>
adjListGraph<TypeOfVer,TypeOfEdge>::adjListGraph(int vSize,const TypeOfVer d[]){
    Vers = vSize;
    Edges = 0;
    verlist = new verNode[vSize];
    for(int i = 0;i < Vers;i ++){
        verlist[i].ver = d[i];
    }
}

析构函数

template <class TypeOfVer, class TypeOfEdge>
adjListGraph<TypeOfVer,TypeOfEdge>::~adjListGraph(){
    edgeNode *p;
    for(int i = 0;i < Vers;i ++){
        while(verlist[i].head){
            p = verlist[i].head;
            verlist[i].head = verlist[i].head->next;
            delete p;
        }
    }
    delete []verlist;
}

邻接表实现

insert操作

template <class TypeOfVer, class TypeOfEdge>
void adjListGraph<TypeOfVer,TypeOfEdge>::insert(TypeOfVer x,TypeOfVer y,TypeOfEdge e){
    int u = find(x);
    int v = find(y);

    verlist[u].head = new verNode(v,w,verlist[u].head);
    ++ Edges;
}

remove操作

template <class TypeOfVer, class TypeOfEdge>
void adjListGraph<TypeOfVer,TypeOfEdge>::remove(TypeOfVer x,TypeOfVer y){
    int u = find(x);
    int v = find(y);
    edgeNode *p = verList[u].head;
    edgeNode *q;
    if(p == nullptr){
        return;
    }
    if(p->end == v){
        verlist[u].head = p->next;
        delete p;
        -- Edges;
        return;
    }
    while(p->next != nullptr){
        if(p->next->end == v){
            break;
        }
        p = p->next;
    }
    if(p->next != nullptr){
        q = p->next;
        p->next = q->next;
        delete q;
        -- Edges;
    }
}

exist操作

template <class TypeOfVer, class TypeOfEdge>
bool djListGraph<TypeOfVer,TypeOfEdge>::exist(TypeOfVer x,TypeOfVer y) const{
    int u = find(x);
    int v = find(y);
    edgeNode *p = verList[u].head;
    while(p != nullptr){
        if(p->end == v){
            break;
        }
        p = p->next;
    }
    if(p == nullptr){
        return false;
    }
    return true;
}

邻接表时间复杂度

图的线性算法，一般指的是O(|V| + |E|)

其他存储方法

• 逆邻接表 将进入同一结点的边组织成一个单链表
• 十字链表 既记录前驱又记录后继 每条边只存储一次
• 邻接多重表 解决无向图中边存储两次的问题