Before：好笑的是，这篇（还有上一篇）似乎上个星期就部署了，现在才开始写，事情也真的是太多了，一度以为上周要死去了😣Obviously，人还活着。期中没有溢出有一点遗憾，但也算满意了。and…放假了！！！第一天陪爸妈在上海玩儿，下午回南京，2号去演唱会，3号一个人去杭州（感觉年龄越大，越喜欢一个人旅行。以前总觉得和朋友家人一起才有意思，上大学后更喜欢一个人待着），4号5号就写写作业吧（主播不要忘了主播的Toy-12306和logic）😢😢😢已经11周了，期末周快来了（那很坏了）

数据结构 11 Graph Traversal

Definition

按照某种次序系统地访问图中的所有顶点，并且使得每个顶点只能被访问一次。

深度优先搜索

• 选中第一个被访问的顶点，并访问
• 依次从顶点的未被访问过的第一个、第二个、第三个…… 邻接顶点出发，进行深度优先搜索
• 如果还有顶点未被访问，则选中一个起始顶点，重新开始上述过程
• 所有的顶点都被访问，则结束

邻接表中公有dfs函数的实现

template <class TypeOfVer,class TypeOfEdge>
void adjListGraph<TypeOfVer,TypeOfEdge>::dfs() const{
    bool *visited = new bool[Vers];

    for(int i = 0;i < Vers;i ++){
        visited[i] = false;
    }

    for(int i = 0;i < Vers;i ++){
        if(visited[i]){
            continue;
        }
        dfs(i,visited);
    }
}

邻接表中私有dfs函数的实现

template <class TypeOfVer,class TypeOfEdge>
void adjListGraph<TypeOfVer,TypeOfEdge>::dfs(int start,bool visited[])const{
    edgeNode *p = verList[start].head;
    visited[start] = true;
    while(p != nullptr){
        if(!visited[p->end]){
            dfs(p->end,visited);
        }
        p = p->next;
    }
}

广度优先搜索

类似于树的层次遍历

过程：

• 选中第一个被访问的顶点；
• 对顶点作已访问过的标志；
• 依次访问已访问顶点的未被访问过的第一个、第二个、第三个……第 m 个邻接顶点
• 如果还有顶点未被访问，则选中一个起始顶点，重复上述过程
• 所有的顶点都被访问到，则结束。

需要一个队列记录哪些结点可以被访问。每次访问一个节点后，将它的后继入队。

邻接表中bfs的实现

template <class TypeOfVer,class TypeOfEdge>
void adjListGraph<TypeOfVer,TypeOfEdge>::bfs() const{
    bool *visited = new bool[Vers];
    int currentNode;
    linkQueue<int> q;
    edgeNode *p;

    for(int i = 0;i < Vers;i ++){
        visited[i] = false;
    }

    for(int i = 0;i < Vers;i ++){
        if(visited[i] == true){
            continue;
        }        
        q.enQueue(i);
        while(!q.empty()){
            currentNode = q.deQueue();
            if(visited[currentNode] == true){
                continue;
            }
            cout << verList[currentNode].ver << endl;
            visited[currentNode] = true;
            p = verList[currentNode].head;
            while(p != nullptr){
                if(visited[p->end] != true){
                    q.enQueue(p->end);
                }
                p = p->next;
            }
        }
    }
}

无向图的连通性

在从任一个结点出发的bfs或dfs结束后，检查其他节点是不是都已被访问

欧拉回路

哥尼斯堡七桥问题

如图：

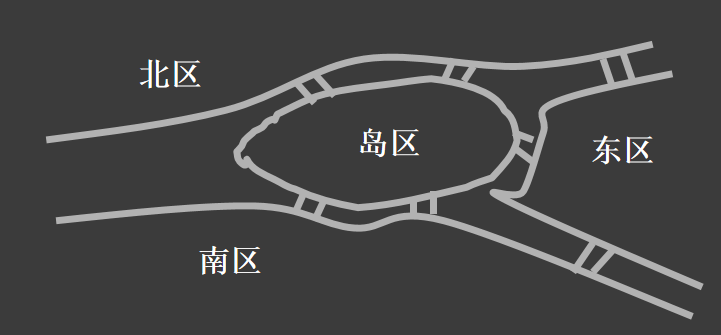
能否找到一条走遍这七座桥，而且每座桥只经过一次，最后又回到原出发点的路径？

抽象一下：

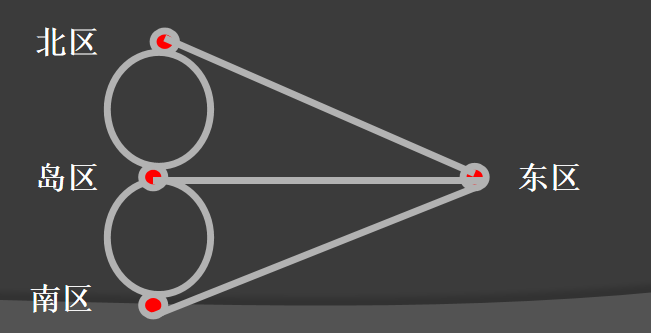
如果有奇数桥的地方不止两个，满足要求的路径是找不到的。如果只有两个地方有奇数桥，可以从这两个地方之一出发，经过所有的桥一次，再回到另一个地方。如果都是偶数桥，从任意地方出发都能回到原点。

欧拉的结论：

• 如果有奇数桥的地方不止两个，满足要求的路径是找不到的。
• 如果只有两个地方有奇数桥，可以从这两个地方之一出发，经过所有的桥一次，再回到另一个地方。
• 如果都是偶数桥，从任意地方出发都能回到原点。

欧拉回路和欧拉路径

• 欧拉路径：图中的一条路径，使得该路径对图的每一条边正好经过一次
• 欧拉回路：起点和终点是相同的欧拉路径

找到欧拉回路的方法 ——— 路径拼接

找出路径上的另外一个尚有未访问的边的顶点，开始另一次深度优先的搜索，将得到的遍历序列拼接到原来的序列中，直到所有的边都已被访问。

首先，检查存在性：检查每个结点的度数是否为偶数

接着，执行一次深度优先的搜索。从起始结点开始，沿着这条路一直往下走，直到无路可走。而且在此过程中不允许回溯。

路径上是否有一个尚有未访问的边的顶点。如果有，开始另一次深度优先的搜索，将得到的遍历序列拼接到原来的序列中，直到所有的边都已被访问。

欧拉回路的实现

• 在邻接表类中增加一个公有成员函数EulerCircuit
• 欧拉回路是由一段一段的路径拼接起来的。为此，设计了一个私有的成员函数EulerCircuit来获得一段回路。
• 公有的函数调用私有的EulerCircuit函数获得一段段的路径，并将它们拼接起来，形成一条完整的欧拉回路。

EulerNode 的定义

struct EulerNode{
    int NodeNum;
    EulerNode *next;
    EulerNode(int val):NodeNum(val),next(nullptr){}
};

当一条边被访问以后，就将这条边删除
Clone函数创建一份邻接表的拷贝，以便在找完路径后能恢复这个图的邻接表

公有EulerCircuit函数实现

template <class TypeOfVer,class TypeOfEdge>
void adjListGraph<TypeOfVer,TypeOfEdge>::EulerCircuit(TypeOfVer start){
    EulerNode *beg,*end,*p,*q,*tb,*te;
    int numOfDegree;
    edgeNode *r;
    verNode *tmp;

    for(int i = 0;i < Vers;i ++){
        numOfDegree = 0;
        r = verList[i].head;
        while(r != nullptr){
            ++ numOfDegree;
            r = r->next;
        }
        if(numOfDegree == 0 || numOfDegree % 2 != 0){
            cout << "No EulerCircuit." << endl;
            return;
        }
    }

    i = find(start);
    tmp = clone();

    EulerCircuit(i,beg,end);
    while(true){
        p = beg;
        while(p->next != nullptr){
            if(verList[p->next->NodeNum].head != nullptr){
                break;
            }
            p = p->next;
        }
        if(p->next == nullptr){
            break;
        }
        q = p->next;
        EulerCircuit(q->NodeNum,tb,te);
        te->next = q->next;
        p->next = tb;
        delete q;
    }

    delete []verList;
    verList = tmp;

    while(beg != nullptr){
        cout << verList[beg->NodeNum].ver << " ";
        p = beg;
        beg = beg -> next;
        delete p;
    }
}

私有EulerCircuit函数实现

template <class TypeOfVer,class TypeOfEdge>
void adjListGraph<TypeOfVer,TypeOfEdge>::EulerCircuit(int start,EulerNode *&beg,EulerNode *&end){
    int nextNode;

    beg = end = new EulerNode(start);
    while(verList[start].head != nullptr){
        nextNode = verList[start].head->end;
        remove(start,nextNode);
        remove(nextNode,start);
        start = nextNode;
        end->next = new EulerNode(start);
        end = end->next;
    }
}

有向图的连通性

深度优先搜索可以测试是否强连通，并找出所有强连通分量
找强连通分量的方法：

• 从任意节点开始深度优先遍历G。对森林中的每棵树进行后序遍历，并按遍历的顺序给每个节点编号
• 将G的每条边逆向，形成Gr。从编号最大的节点开始深度优先遍历Gr。得到的深度优先遍历森林的每棵树就是G的强连通分量。

拓扑排序

存在于有向无环图中
拓扑序列是V中的一个顶点序列V1，V2，…，Vn
满足条件：若在G中，从Vi到Vj有一条路径，则序列中Vi必须排在Vj的前面。

Example：

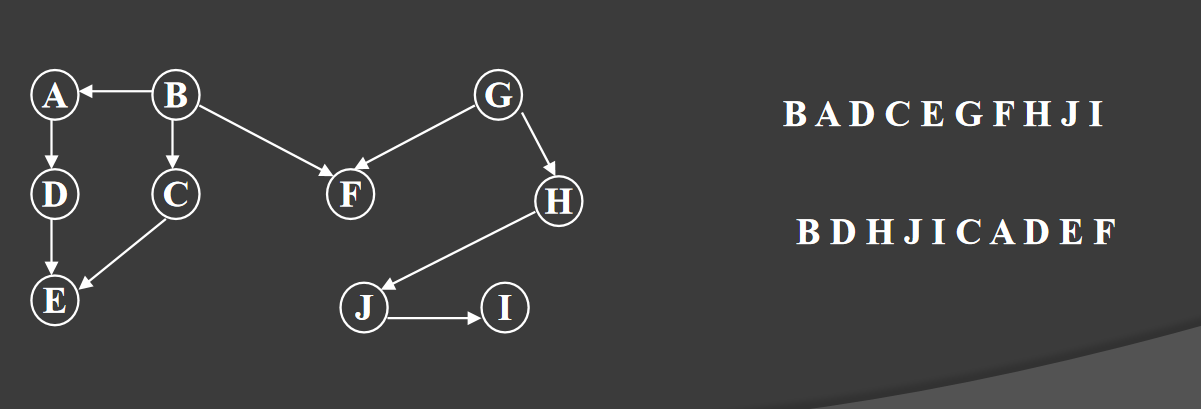
第一个输出的结点（序列中的第一个元素）必须无前驱，即入度为0。无前驱的结点任何时候都可输出；普通结点，必须等到它的所有前驱输出之后才输出

逻辑删除法
当某个节点被输出后，就作为该节点被删除。所有以该节点作为前驱的所有节点的入度减1。

拓扑排序算法总结

• 计算每个结点的入度，保存在数组inDegree中；
• 检查inDegree中的每个元素，将入度为0的结点入队；
• 不断从队列中将入度为0的结点出队，输出此结点，并将该结点的后继结点的入度减1；如果某个邻接点的入度为0，则将其入队。

拓扑排序算法实现

template <class TypeOfVer,class TypeOfEdge>
void adjListGraph<TypeOfVer,TypeOfEdge>::topSort(){
    linkQueue<int> q;
    edgeNode *p;
    int current;
    int *inDegree = new int[Vers];
    for(int i = 0;i < Vers;i ++){
        inDegree[i] = 0;
    }
    for(int i = 0;i < Vers;i ++){
        p = verList[i].head;
        while(p != nullptr){
            ++ inDegree[p->end];
            p = p->next;
        }
    }
    for(int i = 0;i < Vers;i ++){
        if(inDegree[i] == 0){
            q.enQueue(i);
        }
    }

    while(!q.empty()){
        current = q.deQueue();
        cout << verList[current].ver << " ";
        p = verList[current].head;
        while(p != nullptr){
            if(-- inDegree[p->end] == 0){
                q.enQueue(p->end);
            }
        }
    }
}

关键路径

AOV 网络 有向无环图

顶点表示活动，边表示活动的先后次序
主要应用：安排活动的顺序，即拓扑排序

AOE网络 加权有向无环图

• 顶点表示事件，有向边的权值表示某个活动的持续时间，有向边的方向表示活动和事件的先后次序
• 进入顶点的所有活动都结束后，顶点表示的事件发生了，从该顶点出发的所有活动可以开始了

用途：可用于描述整个工程的各个活动之间的关系，活动安排的先后次序
完成整项工程至少需要多少时间：源点到收点的最长路径的长度，称为关键路径。

关键路径算法

找出每个顶点的最早发生时间和最迟发生时间

• 最早发生时间：前面的活动都没有耽误时间，这个事件的发生时间
• 最迟发生时间：不影响整个项目按时完成的前提下，这个事件最晚可以什么时候发生

最早发生时间和最晚发生时间相同的顶点序列构成关键路径

• 最早发生时间：每个直接前驱的最早发生时间加上从该前驱到该顶点的活动时间的最大者

• 最迟发生时间：每个直接后继的最迟发生时间减去顶点到该直接后继的活动时间的最小者就是该顶点的最迟发生时间。

• 找出拓扑序列

• 从头到尾遍历拓扑序列找出结点最早发生时间，从尾到头遍历拓扑序列找到最迟发生时间

• 从头到尾遍历拓扑序列，找出最早发生时间和最迟发生时间的顶点，组成了关键路径。

关键路径算法实现

template <class TypeOfVer,class TypeOfEdge>
void adjListGraph<TypeOfVer,TypeOfEdge>::criticalPath() const{
    TypeOfEdge *ee = new TypeOfEdge[Vers];
    TypeOfEdge *le = new TypeOfEdge[Vers];
    int *top = new int[Vers]; //存储拓扑排序后的序列
    int *inDegree = new int[Vers];
    linkQueue<int> q;
    int i;
    edgeNode *p;
    for(int i = 0;i < Vers;i ++){
        inDegree[i] = 0;
    }
    for(int i = 0;i < Vers;i ++){
        p = verList[i].head;
        while(p != nullptr){
            ++ inDegree[p->end];
            p = p->next;
        }
    }
    for(int i = 0;i < Vers;i ++){
        if(inDegree[i] == 0){
            q.enQueue(i);
        }
    }
    i = 0;
    while(!q.empty()){
        top[i] = q.deQueue();
        p = verList[current].head;
        while(p != nullptr){
            if(-- inDegree[p->end] == 0){
                q.enQueue(p->end);
            }
        }
        i ++;
    }

    for(int i = 0;i < Vers;i ++){
        ee[i] = 0;
    }
    for(int i = 0;i < Vers;i ++){
        p = verList[top[i]].head;
        while(p != nullptr){
            if(ee[p->end] < ee[top[i]] + p->weight){
                ee[p->end] = ee[top[i]] + p->weight;
            }
            p = p->next;
        }
    }

    for(int i = 0;i < Vers;i ++){
        le[i] = ee[top[Vers - 1]];
    }
    for(int i = Vers - 1;i >= 0;i --){
        p = verList[top[i]].head;
        while(p != nullptr){
            if(le[top[i]] + p->weight > le[p->end]){
                le[top[i]] = le[p->end] - p->weight;
            }
            p = p->next;
        }
    }

    for(int i = 0;i < Vers;i ++){
        if(le[top[i]] == ee[top[i]]){
            cout << verList[top[i]].ver << " ";
        }
    }
}