MIT 6.006 Shortest Path Algorithm

MIT 6.006 4 Shortest Path Algorithm

Overview

• Weighted Graph
• General Approaches
• Negative Edges
• Optimal Substructure

Mainly 2 Algorithms：
Dijkstra with O(V + E) for non-negative edge weights
Bellman Ford with O(EV) for general case

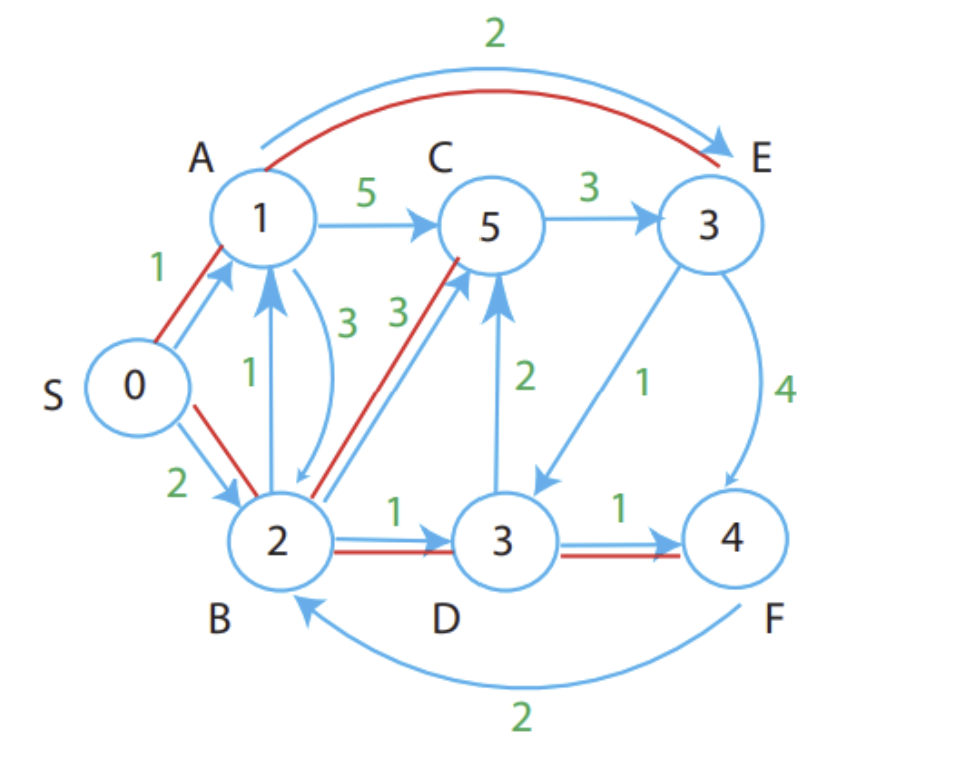
Weighted Graph

Single Source Shortest Paths

Data Structure:
d[v] = value inside circles
= 0 (if v = s) or ∞ (otherwise)
= δ(s,v) (at the end)
with δ(s,v) <= d[v] (all the times)

π[v] = predecessor on the best path to v

Negative-Weight Edges

You may get an endless loop like below:

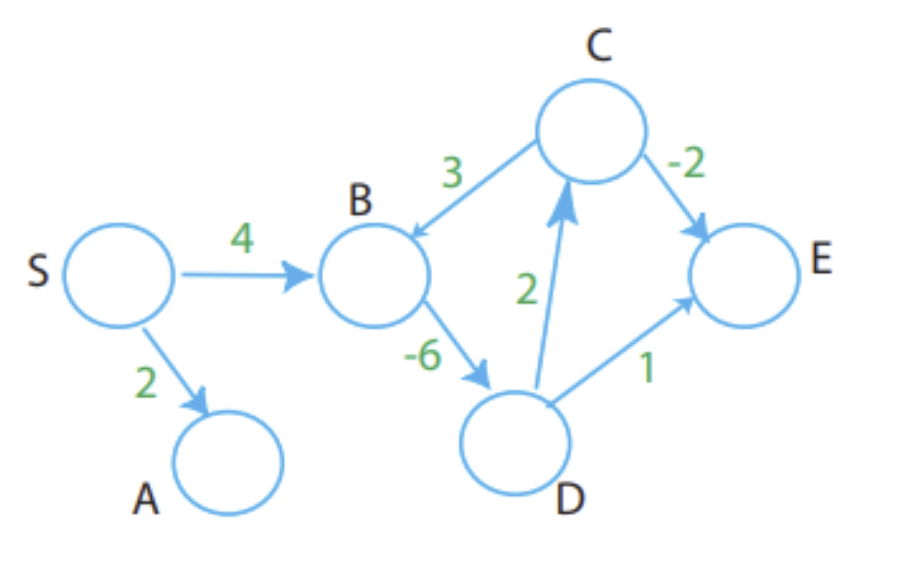
That’s a bad negative circle.

General Structure Of SP Algorithm

Triangle Inequality

Thm:
For all u,v,x $\in$ X, we have

δ(u,v) <= δ(u,x) + δ(x,v)

You may use this idea in Floyd Algorithm.

DAG （Directed Acyclic Graph 有向无环图）

No cycles！

1.Topologically sort the DAG.
2.One pass over vertices in topologically sorted order relaxing each edge that
leaves each vertex.

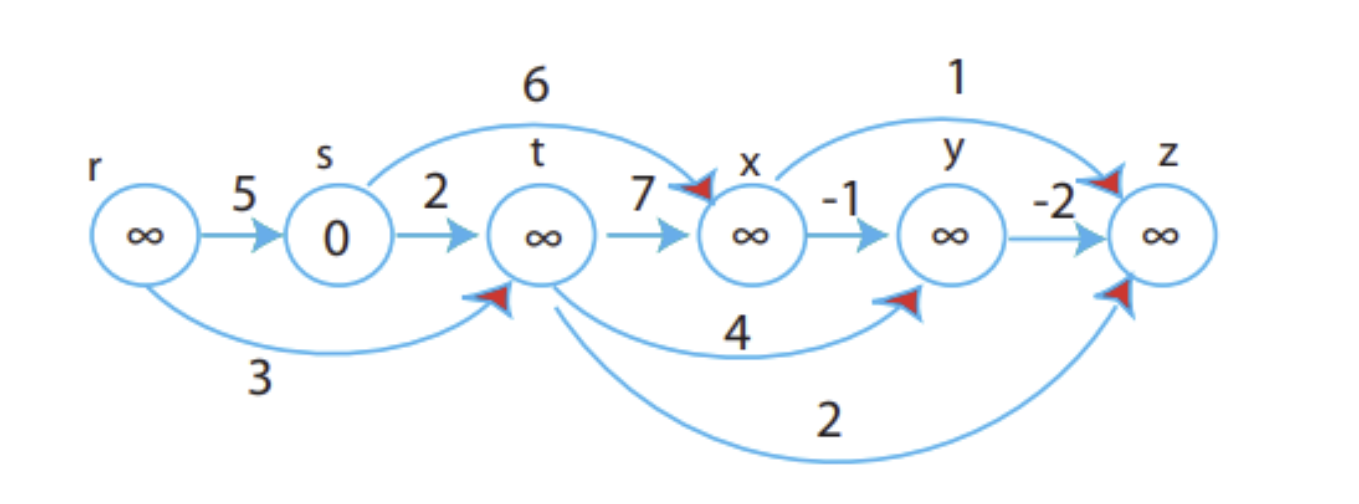
using Dynamic Programming O(V + E)

Dijkstra Algorithm

Core Idea:
For each edge (u, v) $\in$ E, assume w(u, v) ≥ 0, maintain a set S of vertices whose final shortest path weights have been determined. Repeatedly select u $\in$ V − S with minimum shortest path estimate, add u to S, relax all edges out of u.

Pseudo-code

Dijkstra Complexity Analysis

V times : insert into pq
V times : extract min
E times : decrease key

Array

V times : extract min
1 time : decrease key

Total: O(V^2 + E)

Binary Min Heap

lgV times: extract min
lgV times: decrease key

Total: O(VlgV + ElgV)

Fibonacci heap

lgV times: extract min
1 time : decrease key

Total: O(VlogV + E)