Proof of the Undecidabilty of FO

Mathematical Logic 11 Proof of the undecidability of FO

Undecidability of FO

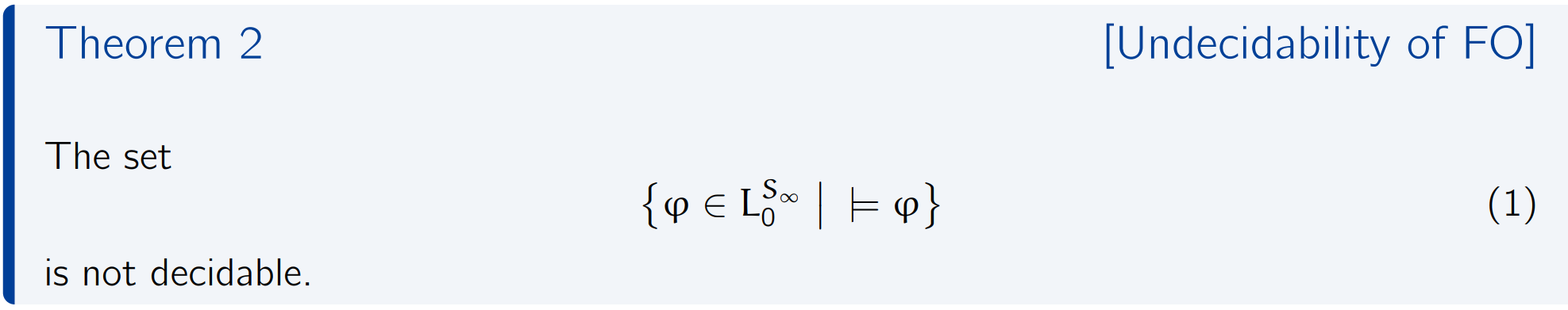
Basic Thoughts of the Proof

We’ve already proved that Π halt is not R-decidable by using Π’halt ⩽m Π halt.

So we only need to show that Π halt ⩽m FO.

i.e We have to construct a reduction.

P: □ -> halt ⇔ |= φP

Main Target: Build φP

Configuration of the Register Machine

引入Configuration 格局的概念

我们定义一个(n + 2) 元组：
(L,m0,m1,…,mn)

L表示当前这一条指令，mi表示第i个寄存器中存储的字符串中 | 的个数（若A = {|}）

显然这样的(n + 2) 元组可以刻画程序的行为

初始状态(0,0,…,0)

停机时状态(k,m0,m1,…,mn)

Reduction Overview 1 : S-Structure

定义一种关系：
R^P := {(L,m0,m1,…,mn) | (0,0,…,0) -> (L,m0,m1,…,mn)}

程序可达格局

So We need that:
1.定义一个公式 ψP decribes R^P
2.P: □ -> halt ⇔ (k,m0,m1,…,mn) $\in$ R^P

所以可以建立如下的S-strcutre

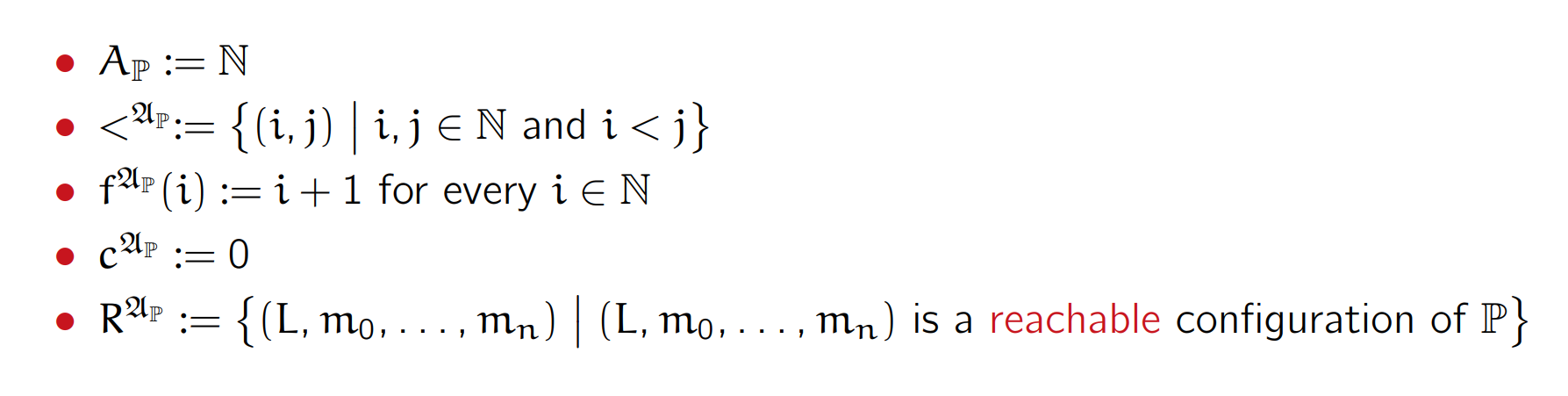
Reduction Overview 2

The desired ψP should satisfy the following two properties:、

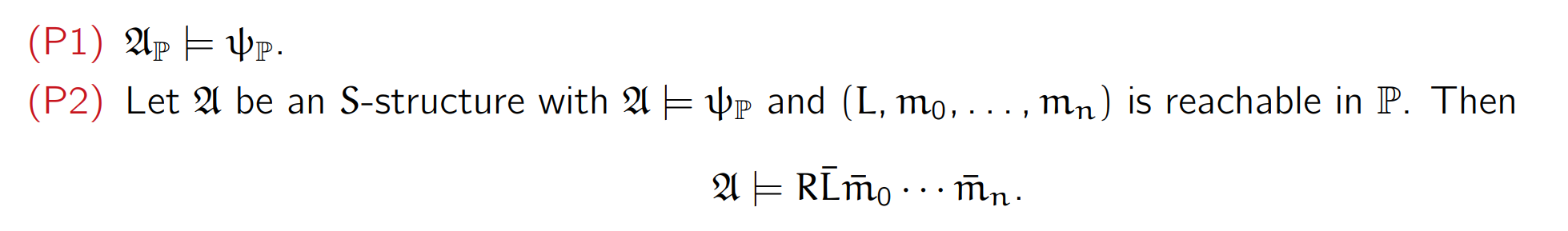
Finally , we set:

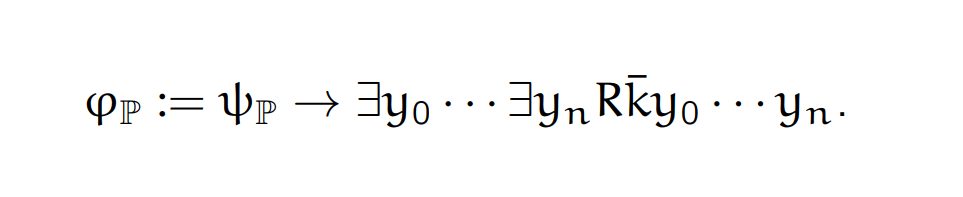
We can easily proved that P: □ -> halt ⇔ |= φP

The Constructuction of ψP

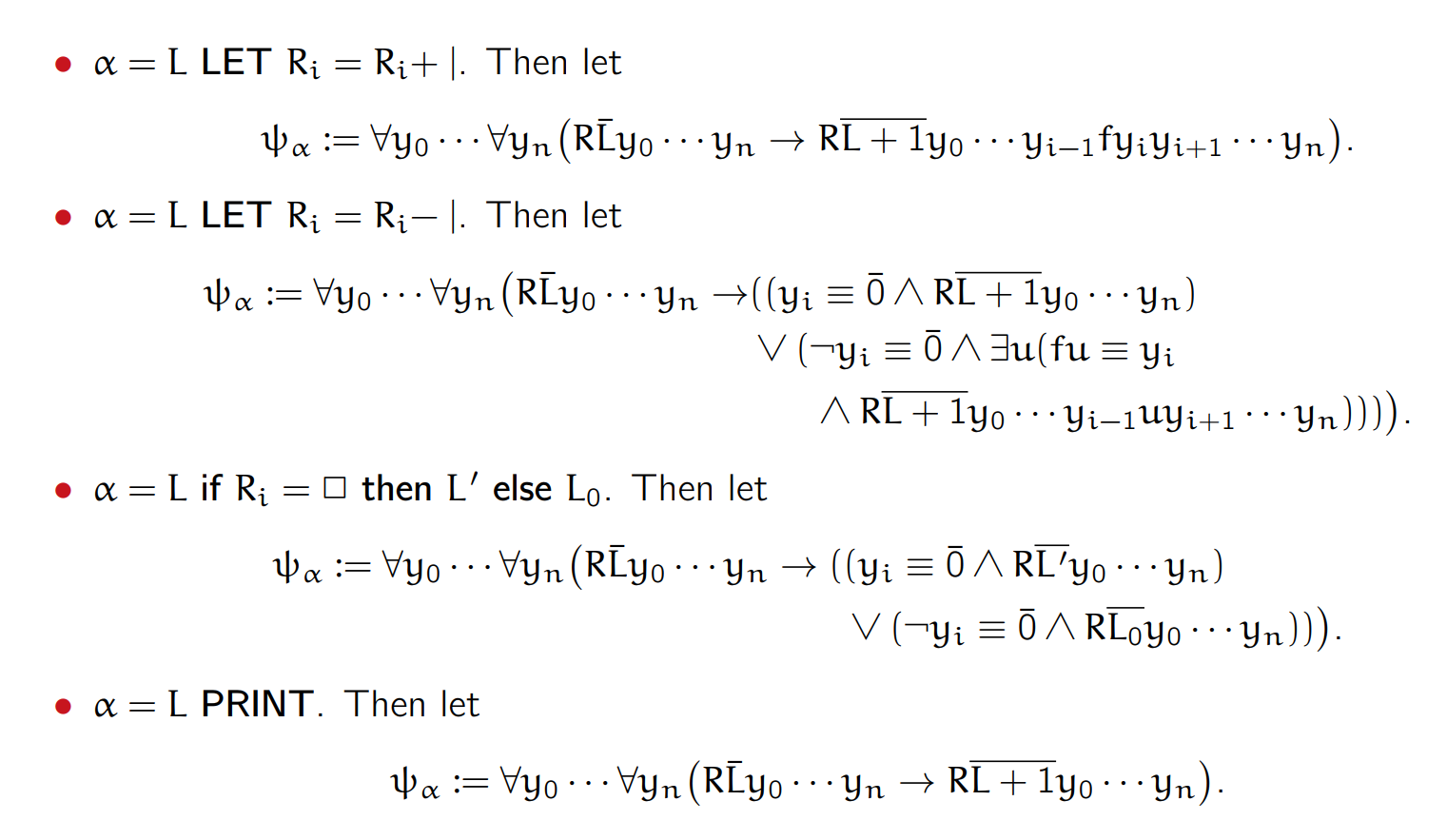
是一个对指令类型的分类讨论