Theories and Decidability

Recall The 4 Questions we’re gonna answer.

Q1: What is a mathematical proof?
Q2: What makes a proof correct?
Q3: Is there a boundary of provability?
Q4: Can computers find proofs?

We’ve already answer Q1 Q2 & Q4.

Now we’re going to answer Q3.

Theories

First, give the definition.

我们还可以定义T 的逻辑闭包：

同样我们还可以知道以下3个命题是等价的

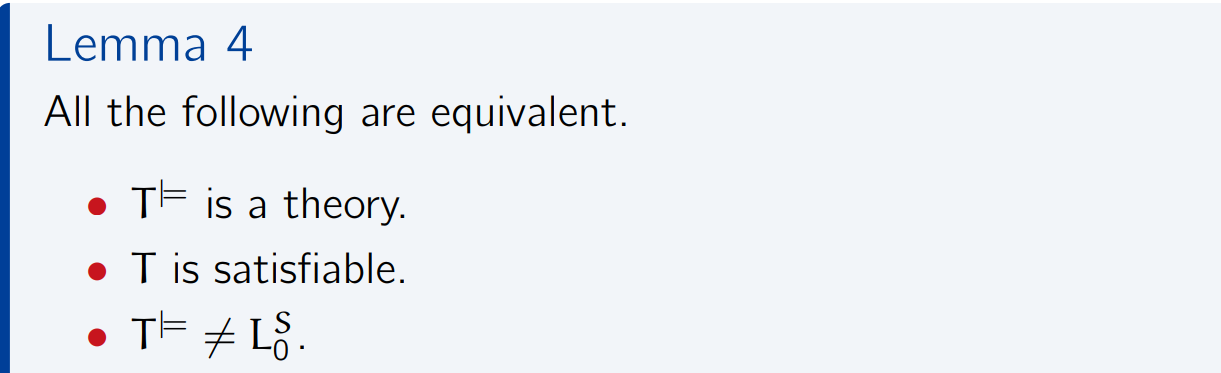
几个证明的关键点在：

• T $\subset$ T⊨ (取任意φ $\in$ T；假设模型M 使得 M ⊨ T，则M ⊨ φ，故T ⊨ φ；所以有φ $\in$ T⊨)
• 取模型M，如果M ⊨ T，可以取一个M无法满足的句子ψ，则ψ 不是T 的逻辑推论，则ψ 不属于T⊨
• T⊨是封闭的，因为对所有的ψ，如果(T⊨) ⊨ ψ，则T ⊨ ψ，则 ψ $\in$ T⊨
• 空真：如果 T 不可满足，且T ⊨ φ，则φ可取任意L^S中公式
• 假设 T⊨ 不可满足，则 (T⊨)⊨ = L^S

Peano Arithmetic

φPA

Elementary arithmetic

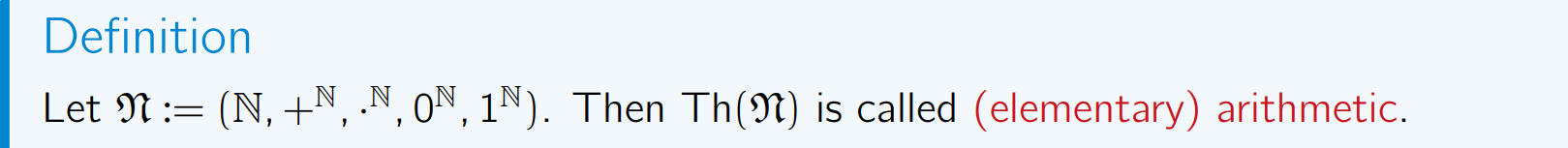
RMK:
It’s easy to see that φPA $\subset$ Th(N),we will show that φPA ⊊ Th(N)

R-axiomatizable 可公理化

Theorem 5

Every R-axiomatizable theory is R-enumerable.

Complete Theory

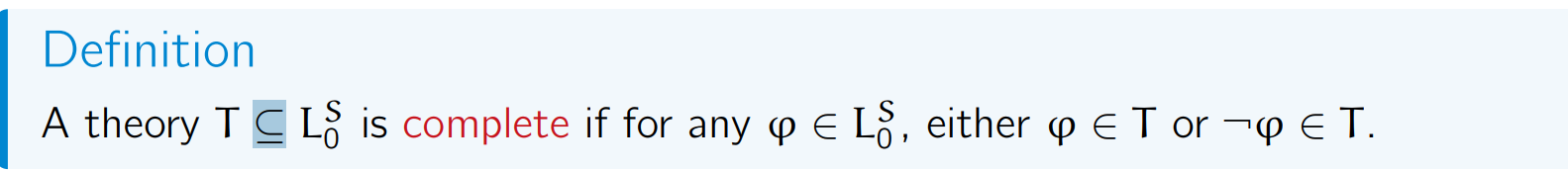
Theorem 6

(i) Every R-axiomatizable complete theory is R-decidable.
(ii) Every R-enumerable complete theory is R-decidable.