Graph Algorithm

Graph Algorithms

ps: 上机课是05.18上的，算法是05.23学的🤣（评价是这周事还是太多了）perhaps和这节上机课量巨大也有关系吧😢

术语回顾

  • DAG 有向无环图
  • 点度 = 入度 + 出度
  • SPT 最短路径树

最短路 单源/多源

Q：给出一个加权图和图上的一个节点s，找出s到图中每一节点的最短路径

Dijkstra 算法

Core:
v=argmin_u∈SPT,(u,v)∈E,v∉SPT{d(s,u)+w(u,v)}

代码实现（使用pq进行优化）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <iostream>
#include <queue>
struct edge{
    edge *next;
    int end;
    int weight;
};
struct ver{
    edge *head;
};
ver G[200005];
void add_edge(int u,int v,int w){
    edge *current = new edge;
    current->end = v;
    current->weight = w;
    current->next = G[u].head;
    G[u].head = current;
}
bool known[200005];
int distance[200005];
struct Pair{
    int dis;
    int u;
    bool operator<(const Pair &a)const{
	return dis > a.dis;
    }
};
priority_queue<Pair> pq;
int main(){
    int n,m;
    int start;
    int u,v,w;
    cin >> start;
    for(int i = 1;i <= m;i ++){
        cin >> u >> v >> w; 
        add_edge(u,v,w);
    }
    for(int i = 1;i <= n;i ++){
        known[i] = false;
        distance[i] = 1e9;
    }
    distance[start] = 0;
    pq.push({0,start});
    while(!pq.empty()){
        Pair top = pq.top();
        pq.pop();
        if(known[top.u]){
            continue;
        }
        known[top.u] = true;
        edge *current = G[top.u].head;
        while(current){
            if(dis[current->end] > dis[top.u] + current->weight){
                dis[current->end] = dis[top.u] + current->weight;
                pq.push({dis[current->end],current->end});
            }
            current = current->next;
        }
    }
}

upd：改了一下Dijkstra的板子（某个🤡机考的时候Dijkstra板子写成了修改前的错误版本导致痛失70分😭😭😭）。
总结：板子写错最为致命🫠🫠🫠 逆天机考至少有170分的😅😅😅

Bellman-Ford 算法

用于处理存在负边的图
update操作的正确性毋庸置疑
于是，假设d(s,v)最短路经过k个点，那么在经过(k-1)个点的最短路都被确定的前提下，一次update操作保证了d(s,v)的正确性

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <iostream>
struct edge{
    edge *next;
    int end;
    int weight;
};
struct ver{
    edge *head;
};
ver G[200005];
void add_edge(int u,int v,int w){
    edge *current = new edge;
    current->end = v;
    current->weight = w;
    current->next = G[u].head;
    G[u].head = current;
}
int distance[200005];
int main(){
    int n,m;
    int start;
    int u,v,w;
    cin >> start;
    for(int i = 1;i <= m;i ++){
        cin >> u >> v >> w; 
        add_edge(u,v,w);
    }
    for(int i = 1;i <= n;i ++){
        known[i] = false;
        distance[i] = 1e9;
    }
    distance[start] = 0;
    bool flag = false;
    for(int i = 1;i <= n;i ++){
        flag = false;
        for(int j = 1;j <= n;j ++){
            if(dis[current] == 1e9){
                continue;
            }
            edge *current = G[j].head;
            while(current){
                if(dis[curent->end] > dis[j] + current->weight){
                    dis[current->end] = dis[j] + current->weight;
                    flag = true;
                }
                current = current->next;
            }
        }
        if(!flag){
            break;
        }
    }
    if(!flag){
        std::cout << -1;//存在负权环
    }
    return 0;
}

SPFA 算法 （已经死了）

虽然可以构造数据把BF的队列优化卡掉，但还是学习一下这种优化吧，毕竟笔者刚做小作业时，第一遍BF 大T特T，第二遍SPFA 被卡了一个点，最后进行了SPFA + SLF优化才过。

首先是SPFA的队列优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
bool visit[25005];//用于维护结点是否上次被松驰过，因为只有上一次被松弛过的结点才会对下一轮循环产生影响
queue<int> q;

while(!q.empty()){
    int u = q.front();
    q.pop();
    visit[u] = false;
    edge *current = G[u].head;
    while(current){
        if(dis[current->end] > dis[u] + current->weight){
            dis[current->end] = dis[u] + current->weight;
            if(!visit[current->end]){
                visit[current->end] = true;
                q.push(current->end);
            }
        }
        current = current->next;
    }
}

我们继续观察，还可以发现，如果松驰后的顶点的dis越小，那么对后续产生的影响越大，可以往前放，于是我们首先想到是否可以用pq解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
dis[s] = 0;
priority_queue<int> q;
q.push(s);
while(!q.empty()) {
    int u = q.top();
    q.pop();
    visit[u] = false;
    edge *current = G[u].head;
    while (current) {
        if(dis[current->end] > dis[u] + current->weight) {
            dis[current->end] = dis[u] + current->weight;
            if(!visit[current->end]) {
                q.push(current->end);
                visit[current->end] = true;
            }
        }
        current = current->next;
    }
}

确实优化了，但依然被助教卡了，主要还是因为pq凭空多了调整的logN级复杂度，那么还能怎么优化呢？

男明星：deque！双端队列使插入删除变为O(1)的复杂度，很好了🥰

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
dis[s] = 0;
deque<int> q;
q.push_front(s);
while(!q.empty()) {
    int u = q.front();
    q.pop_front();
    visit[u] = false;
    edge *current = G[u].head;
    while (current) {
        if(dis[current->end] > dis[u] + current->weight) {
            dis[current->end] = dis[u] + current->weight;
            if(!visit[current->end]) {
                visit[current->end] = true;
                if(!q.empty() && dis[current->end] < dis[q.front()]){
                    q.push_front(current->end);
                }else{
                    q.push_back(current->end);
                }
            }
        }
        current = current->next;
    }
}

这也就是传说中的 SPFA + SLF优化！妙啊！（使我不用写Dijkstra + 连通分量的正解了XD）

Floyd 算法

用于多元最短路问题（求任意两个结点之间最短路）
复杂度较高但常数小

类似BF的dp思路，维护一个三维数组 d[k,u,v]，表示只允许经过 1-k 的顶点，结点u到结点v 的最短路长度

状态转移方程为：
d[k,u,v] = min{d[k-1,u,v], d[k-1,u,k] + d[k-1,k,v]}

从 u 到 v 经过 k 或者不经过 k

代码实现：

1
2
3
4
5
6
7
for(int k = 1;k <= n;k ++){
    for(int u = 1;u <= n;u ++){
        for(int v = 1;v <= n;v ++){
            f[k][u][v] = min(f[k - 1][u][v],f[k - 1][u][k] + f[k - 1][k][v]);
        }
    }
}

例题

贴个题: 裂点

省流：

1
n 个点 m 条有向边，边有正边权，可以免费走 k 条边，边权视为 0，求 s 到 t 的最短路

想法：
点集取为(v,f)，f 为免费次数

则(u,f) -> (v,f) 边权w
(u,f) -> (v,f - 1) 0

用Dijkstra即可

连通分量

Concept Recall

  • 连通性是二元等价关系（自反性、对称性、传递性）
  • 有向图中，弱连通：转向无向图后连通；
    强连通：任意两点间相互可达
  • 强连通分量（SCC）是等价类，将点集划分成若干个内部强连通的部分

强连通分量算法

Kosaraju 算法

  • 从任意结点开始对有向图进行深度优先搜索，得到一个深度优先森林
  • 将节点遍历：按照生成树的次序 + 对每一棵树上的节点进行后序遍历
  • 将图 G 逆向得到Gr
  • 从编号最大的节点开始深度优先搜索，得到的森林就是原图的强联通分量。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <iostream>
#include <vector>
using namespace std;
struct edge {
    edge *next;
    int end;
    int weight;
};
struct ver {
    edge *head;
};
ver G1[25005];//正向图
ver G2[25005];//反图
void add_edge1(int u,int v,int c) {
    edge *current = new edge;
    current->end = v;
    current->weight = c;
    current->next = G1[u].head;
    G1[u].head = current;
}
void add_edge2(int u,int v,int c) {
    edge *current = new edge;
    current->end = v;
    current->weight = c;
    current->next = G2[u].head;
    G2[u].head = current;
}
int n,m;
bool visit[25005];
bool colored[25005];
vector<int> s;
int SCCcnt;
void dfs1(int u){
    visit[u] = true;
    edge *current = G1[u].head;
    while(current){
        if(!visit[current->end]){
            dfs1(current->end);
        }
        current = current->next;
    }
    s.push_back(u);
}
void dfs2(int u){
    colored[u] = SCCcnt;
    edge *current = G2[u].head;
    while(current){
        if(!colored[current->end]){
            dfs2(current->end);
        }
        current = current->next;
    }
}
int main(){
    cin >> n >> m;
    for(int i = 1;i <= m;i ++){
        int u,v,w;
        cin >> u >> v >> w;
        add_edge1(u,v,w);
        add_edge2(v,u,w);
    }
    for(int i = 1;i <= n;i ++){
        if(!visit[i]){
            dfs1(i);
        }
    }
    for(int i = n;i >= 1;i --){
        //从栈顶开始向前回溯
        if(!colored[s[i]]){ //还未被分配到任何SCC中
            ++ SCCcnt;
            dfs2(s[i]);
        }
    }
}

Tarjan 算法

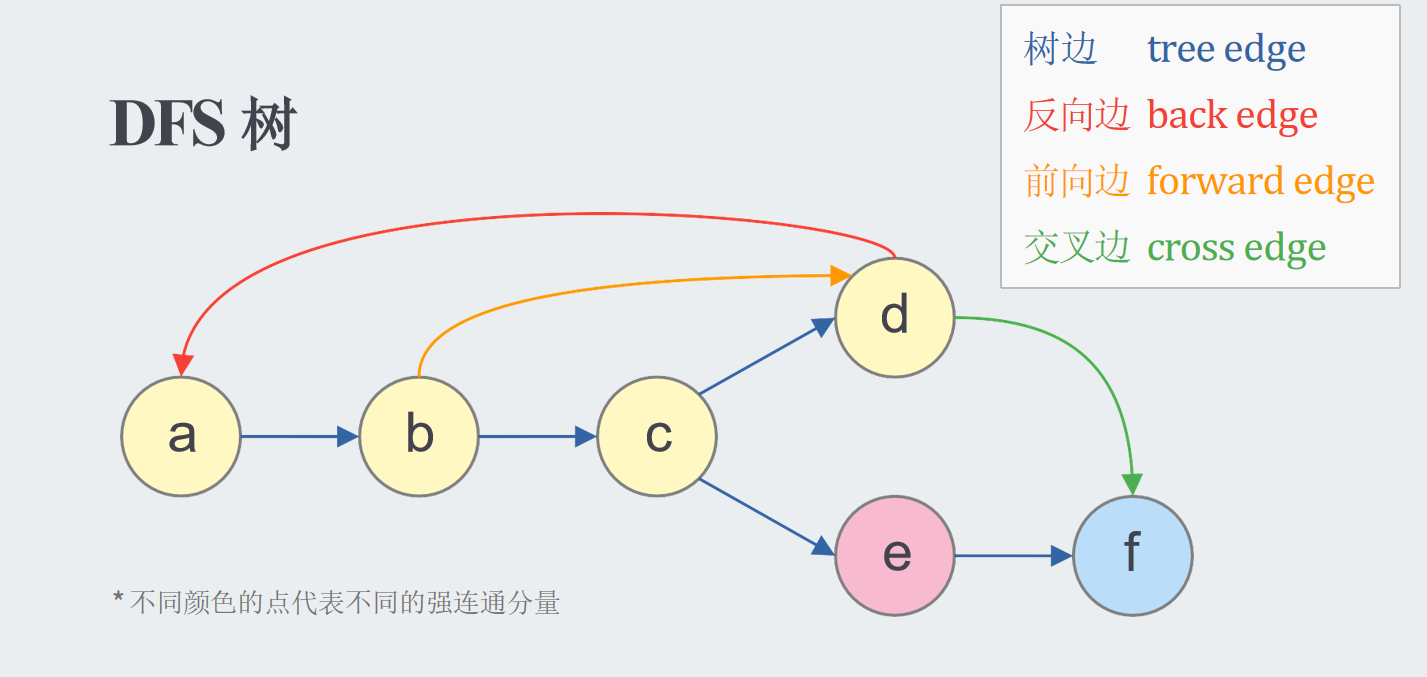
在DFS过程中，按照生成的顺序会生成一颗结构良好的DFS树。DFS得到的序列（DFS序并不能保证相邻节点一定有边相连），但是DFS树的节点一定都是图中的节点，换句话说，DFS树在本质上就是一个在中序遍历上完全等价的树。
DFS Tree

但是很显然，一颗DFS树上的顶点不代表联通。我们需要考虑不在DFS树上的边，例如这里的：

  • 反向边
  • 前向边
  • 交叉边（横向边）

Lemma: SCC 中 dfn 最小的结点是该 SCC 中所有节点在 DFS 树上的祖先（也就是所谓最远能到达的祖先）

Tarjan 算法实现

用一个栈表示没有全部访问的 SCC
记录 DFS 序 dfn[v] 和最远能走到的栈中节点 low[v]
要求：从 v 到 low[v] 的路径中最多一条非树边

Tarjan 实现

一个点的所有边访问结束之后，若 dfn[v ] = low[v ] ，则 v 及其子树的一部分构成一个 SCC
Lemma: dfn[v] = low[v] 的点是其所在 SCC 中 dfn 最小的点
若不是，则 v 到达之要经过非树边，v 必然能通过仅一条非树边到达dfn更小的点

Tarjan算法的原理是笔者学过所有算法中最恶心最绕的😅，但它的实现还是挺容易的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int dfn[200005];
int low[200005];
int dfnCnt;
int Stack[200005];//一个栈，用于跟踪当前正在进行 DFS 遍历的路径上的节点。节点在被发现时入栈，在找到一个强连通分量时出栈
bool inStack[200005];//是否在栈中
int top;//栈顶指针
int scc[200005];//结点i所在强连通分量编号
int sccCnt;//强连通分量个数计数器
int sz[200005];//强连通大小

void Tarjan(int u){
    low[u] = dfn[u] = ++dfnCnt;
    Stack[++ top] = u;
    inStack[u] = true;
    edge *current = G[u].head;
    while(current){
        if(!dfn[current->end]){
            Tarjan(current->end);
            low[u] = min(low[u],low[current->end]);
        }else if(inStack[current->end]){
            low[u] = min(low[u],dfn[current->end]);
        }
        current = current->next;
    }
    if(dfn[u] == low[u]){
        //找到SCC祖先结点
        ++sccCnt;
        do{
            scc[STACK[top]] = sccCnt;
            sz[sccCnt] ++;
            inStack[Stack[top]] = false;
        }while(Stack[top --] != u);
    }
}

int main(){
    for(int i = 1;i <= n;i ++){
        if(!dfn[i]){
            Tarjan(i);
        }
    }
}

一道很棒的Tarjan例题（算是自己做出来的一道蓝题吧）

老规矩，贴题，ATM

相当综合的一题，把笔者今天学的近乎所有图算法都用了一遍🤣🤣🤣
想法是缩点，也就是求所有强连通分量（Tarjan板子），看成一张新的图（此图是DAG），于是使用SPFA求最长路径。特别要注意的是，不可以用Dijkstra，因为贪心的思想放在最长的情况下并不正确！！！（笔者在AC后尝试用Dijkstra WA 了2个点）

贴个AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
#include <iostream>
#include <queue>
using namespace std;
int n,m;
int s,p;
int sccCnt;
int SCC[500005];
int Stack[500005];
int top;
int dfn[500005];
int dfnCnt;
int low[500005];
bool inStack[500005];
int Money[500005];//每个路口的钱
int sccMoney[500005];//每个强连通分量中抢到钱的总数
bool sccPub[500005];//每个强连通分量中是否有pub
bool pub[500005];//酒吧位置
struct edge {
    edge *next;
    int end;
};
struct ver {
    edge *head;
};
ver G[500005];
void add_edge(int u,int v) {
    edge *current = new edge;
    current->end = v;
    current->next = G[u].head;
    G[u].head = current;
}
void tarjan(int u) {
    low[u] = dfn[u] = ++dfnCnt;
    inStack[u] = true;
    Stack[++top] = u;
    edge *current = G[u].head;
    while(current) {
        if(!dfn[current->end]) {
            tarjan(current->end);
            low[u] = min(low[u],low[current->end]);
        }else if(inStack[current->end]) {
            low[u] = min(low[u],dfn[current->end]);
        }
        current = current->next;
    }
    if(dfn[u] == low[u]) {
        ++sccCnt;
        do {
            inStack[Stack[top]] = false;
            SCC[Stack[top]] = sccCnt;
            sccMoney[sccCnt] += Money[Stack[top]];
            if(pub[Stack[top]]) {
                sccPub[sccCnt] = true;
            }
        }while (Stack[top --] != u);
    }
}
ver newG[500005];
void add_edgeNEW(int u,int v) {
    edge *current = new edge;
    current->end = v;
    current->next = newG[u].head;
    newG[u].head = current;
}
int dis[500005];
bool visit[500005];
int main() {
    cin >> n >> m;
    for(int i = 1;i <= m;i ++) {
        int u,v;
        cin >> u >> v;
        add_edge(u,v);
    }
    for(int i = 1;i <= n;i ++) {
        cin >> Money[i];
    }
    cin >> s >> p;
    for(int i = 1;i <= p;i ++) {
        int pos;
        cin >> pos;
        pub[pos] = true;
    }
    for(int i = 1;i <= n;i ++) {
        if(!dfn[i]) {
            tarjan(i);
        }
    }
    for(int i = 1;i <= n;i ++) {
        edge *current = G[i].head;
        int nCurrent = SCC[i];
        while(current) {
            int nEnd = SCC[current->end];
            if(nEnd != nCurrent){
                add_edgeNEW(nCurrent,nEnd);
            }
            current = current->next;
        }
    }
    int start = SCC[s];//起始强连通分量
    queue<int> q;
    q.push(start);
    dis[start] = sccMoney[start];
    while(!q.empty()) {
        int top = q.front();
        q.pop();
        visit[top] = false;
        edge *current = newG[top].head;
        while(current) {
            if(dis[current->end] < dis[top] + sccMoney[current->end]) {
                dis[current->end] = dis[top] + sccMoney[current->end];
            }
            if(!visit[current->end]) {
                visit[current->end] = true;
                q.push(current->end);
            }
            current = current->next;
        }
    }
    int MaxMoney = 0;
    for(int i = 1;i <= sccCnt;i ++) {
        if(sccPub[i]) {
            if(dis[i] > MaxMoney) {
                MaxMoney = dis[i];
            }
        }
    }
    cout << MaxMoney;
    return 0;
}

Reference

Thanks so much:

Final Words

做完了最后一次小作业的最后一题，再加上周四已经通过的火车票管理系统，数据结构CS1951 的所有课程内容都基本完成了（还有个机考😭）。感觉一学期下来代码能力得到了不小的提升（虽然这学期好像也没写什么代码🤣）。有一点怅然若失，每天写学算法、写小作业、debug大作业的日子就这样过去了，但想到未来还会学更多有趣的东西，又觉得很兴奋。或许一年前的我，还在为差一点点就能去清北，而质疑自己的选择，但我想我不会后悔我做的每一个决定。也有人问我家那么富为什么要来学cs😅，但我对钱真的不感兴趣呢。一直认为自己物欲很低（室友锐评：清心寡欲），没什么特别想要的，花钱很少，觉得钱没那么重要，也不想靠父母活一辈子（如果我这么选，我甚至不用上大学😅）。

Algorithms
#Algorithm #Dijkstra #Bellman Ford #Floyd #SPFA #SLF #Tarjan #Kosaraju
Graph Algorithm
https://janezair.site/2025/05/23/AlgorithmOfDS5/
Author
Yihan Zhu
Posted on
May 23, 2025
Updated on
May 26, 2025
Licensed under